Fixed-point atan2

2012/12/27

First published February 6, 2012 then taken down for revision. Updated further in January 2017 to correct errors and expand explanations.

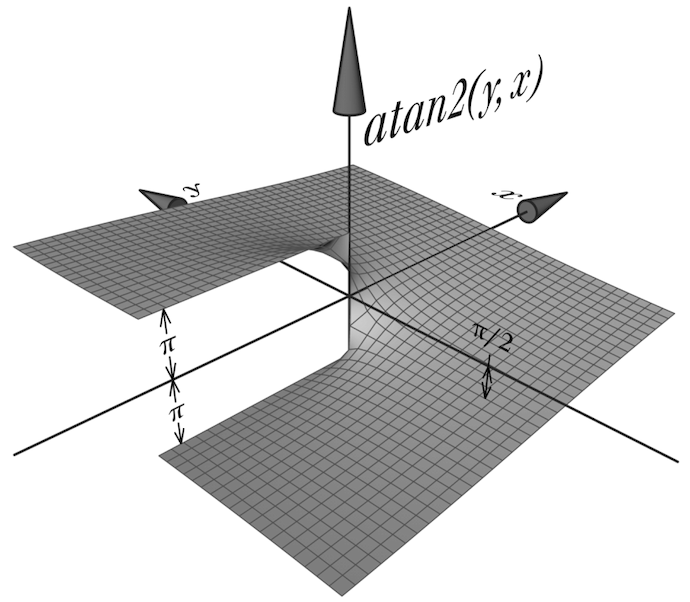
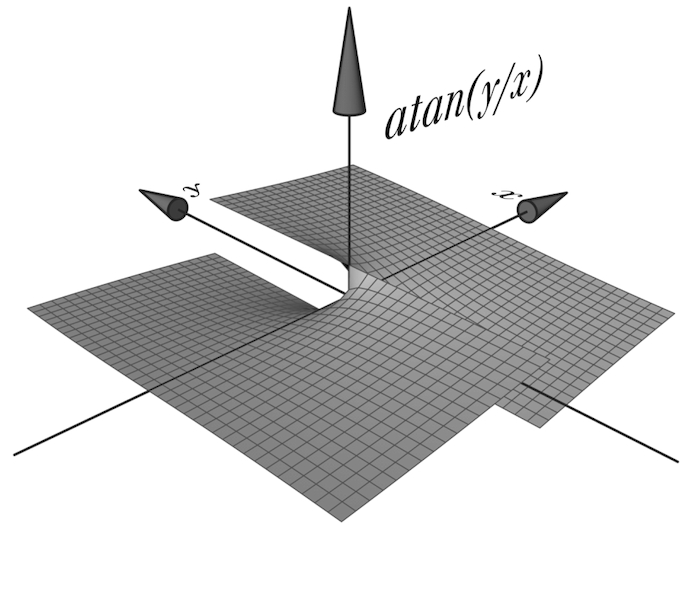
atan2 is a freaking useful function: given some y and x^*, it computes their “four-quadrant” arctangent^†, which is basically that coordinate’s angle in polar form.

These two beautiful Wikipedia diagrams explain why it’s so much better than the naïve atan(y/x):

It also shows the reasons why I suffered a stroke of unsanity and whipped up my own atan2 function in Q15 fixed point/1.0.15/1.15/whycan’twehaveonenameforthis format that’s so commonly used by DSP chips:

You see how smooth that thing is? That’s because it was generated in some high-falutin’ floating point on a fancy machine with a sweet FPU. Well, I program itty-bitty embedded microcontrollers with nary a hardware integer divider, so I use fixed-point arithmetic for my math. One of the more popular fixed-point formats is Q15, which is taking a 16-bit signed two’s complement integer^‡ and instead of having it represent $[- 32768, 32767]$ , have it represent $[- 1, 1 - 2^{- 15}]$ ^§. I used it out of convenience since I knew a few of the tricks for making Q15 computations go fast.
The range on atan2 output is $[- π, π]$ . That’s nice and mathemagicatical, but not so useful an angle representation on a microcontroller. See, first, that doesn’t fit inside of a Q15 number. Then even if it did, it’d still be wasteful to have your angle’s range be bookended by transcendental numbers. You got only 16 bits! You want every possible 16-bit number to be a valid and useful angle, evenly covering the whole range of possible angular positions still without redundancy. For example, there shouldn’t be different representations for both $\frac{2}{3} π$ and $- \frac{4}{3} π$ , since they’re the same angular position. So, let’s map our 16-bit range $[- 2^{15}, 2^{15} - 1]$ or $[- 32768, 32767]$ to (almost) a full turn of the circle $[- \frac{2^{15}}{2^{16}} turns, \frac{2^{15} - 1}{2^{16}} turns]$ which is really $[- \frac{1}{2} turns, \frac{32767}{65536} turns]$ .

Fixed point angular representation §

A turn here is of course a rotation of $2 π$ radians, so all this mapping does is assign a scaling factor between radians and 16-bit numbers in a unit we’ll call binary radians, or brads. Specifically, between one turn’s worth of radians and the whole 16-bit space’s worth of brads.

angle in radians = \frac{2 π rad}{2^{16} brad} \times angle in binary

However, this particular factor does more than only preserve precision. It aligns the overflow boundary of 16-bit integers to the wrapping that happens to angles each turn. It elegantly exploits the modular arithmetic property of binary numbers to provide angle wrapping and canonicalization. Just like adding 1° to 359° gives 0°, adding 1 to 32767 fixed point units gives −32768 fixed point units.

This avoids having to perform modulo during angle computations to keep them “in range,” including the fairly expensive fmod.

Even more conveniently, signed binary integers can be converted to and from unsigned “for free,” as they are simply different ways to interpret the same bit pattern. Guess what? This works perfectly on angles in brads because it’s analogous to converting between $[- π, π)$ and $[0, 2 π)$ . As an example, let’s say you have the angle $\frac{4}{3} π$ , initially represented as 43691 brads:

\begin{aligned} \frac{4}{3} π rad \times \frac{2^{15} brad}{π rad} & =43691brad \\ \equiv-21845 \\ =-21845brad\times\frac{π rad}{2^{15} brad} \\ \approx0.66666πrad \\ \approx-\frac{2}{3}πrad \end{aligned}

Free conversions of angles to non-negative values and automatic rotation wrapping are incredibly powerful for digital computation. We can do wicked fast things like limited-precision sin and cos lookup tables:

const int16_t sin_lut[4096]; // a 2^12 table of precomputed sin values
const uint16_t angle; // angle in 16-bit binary radians

// right shift because there are 16x possible angles as table entries
const int16_t sin_of_angle = sin_lut[angle >> 4];

// cos(x) = sin(x + pi / 2), pi / 2 rad = 16384 brad
const int16_t cos_of_angle = sin_lut[(angle + 16384) >> 4];

// we can also round to the nearest entry
const int16_t sin_of_rounded_angle = sin_lut[(angle + (1 << 3)) >> 4];

// or linearly interpolate between them
const int16_t lower = sin_lut[angle >> 4];
const int16_t upper = sin_lut[(angle >> 4) + 1];
const int16_t angle_fraction = (angle & 0xF) << (15 - 4);
const int16_t better_sin = lerp(lower, upper, angle_fraction);

Note that the contents of the int16_t numbers above are not bradians, but “normal” Q15 fixed point numbers representing the range $[- 1, 1 - 2^{- 15}]$ .

Implementing `atan2` §

Given that $atan2 (x, y) = arctan (\frac{y}{x})$ when $x, y$ are in quadrants I and IV, I can implement atan2 using arctangent near zero, where it’s smooth and easily approximated. Inputs outside of that domain can be manipulated into it, provided that the output is adjusted for those manipulations.

“Derive” arctangent approximation §

To implement atan2, I whipped out Chapter 18 from Streamlining Digital Signal Processing, which had several approximations for atan, including the following formula:

\begin{aligned} {arctan}^{⋆} (x) & =\frac{π}{4}x+0.273x(1-|x|) \\ \approxarctan(x),x\in[-1,1] \end{aligned}

That’s a local polynomial^¶ approximation good to a worst-case error of 0.22° for $- 1 \leq x \leq 1$ .

Convert units §

Now this is single-operand arctangent, so its parameter $x$ is really the slope $\frac{y}{x}$ as understood by atan2. Hence, the limited domain of the approximation function is equivalent to octants I and VIII in terms of atan2^♠. The range is $[- \frac{π}{4}, \frac{π}{4}]$ over that domain. We want to convert to turns, since that’s bit easier to work with:

\begin{aligned} {arctan}_{τ}^{⋆} (x) & =\frac{1}{2 π}{arctan}^{⋆}(x) \\ =\frac{1}{2 π}(\frac{π}{4} x + 0.273 x (1 - | x |)) \\ =\frac{1}{8}x+\frac{0.273}{2 π}x(1-|x|) \\ =x(\frac{1}{8} + \frac{0.273}{2 π} - \frac{0.273}{2 π} | x |) \end{aligned}

Now the range is $[- \frac{1}{8}, \frac{1}{8}]$ in units of turns (or τ). The last form requires only two multiplications and one addition as opposed to the three multiplications and two additions required by the original form.

One more thing: because the final function takes in operands with a range of

y, x \in [- 1, 1)_{Q 15}

in Q15 format and I want its output angle be one turn

θ \in {[- \frac{1}{2}, \frac{1}{2})}_{τ}

in 16-bit brads, I actually need to scale the approximation back up to deal with the 1.15→0.16 fixed point conversion:

\begin{aligned} {arctan}^{†} (x) & =2{arctan}_{τ}^{⋆}(x) \\ =x(\frac{1}{4} + \frac{0.273}{π} - \frac{0.273}{π} | x |) \end{aligned}

Exploit function symmetries §

To handle inputs not in octant I and VIII, I chose to manipulate the coordinates and exploit the symmetries of atan2. For example, if our input is in octants II and III, then we rotate it by −90°:

\begin{aligned} [\begin{array}{c} x^{'} \\ y^{'} \end{array}] & =[\begin{array}{c} \cos - 90 ° & - \sin - 90 ° \\ \sin - 90 ° & \cos - 90 ° \end{array}][\begin{array}{c} x \\ y \end{array}] \\ =[\begin{array}{c} 0 & 1 \\ - 1 & 0 \end{array}][\begin{array}{c} x \\ y \end{array}] \\ =[\begin{array}{c} y \\ - x \end{array}] \end{aligned}

Now x′ and y′ are in octants I and VIII—as required—and we can pass them to our approximate arctangent:

{arctan}^{†} (\frac{y^{'}}{x^{'}})

The result then needs to be rotated 90° to put it back into octants II and III. This is easy since the result is already in angular units: just add 90°. Altogether, it looks like this:

\begin{aligned} atan2 (y, x) & ={arctan}^{†}(\frac{y^{'}}{x^{'}})+90° \\ ={arctan}^{†}(\frac{- x}{y})+90° \\ =90°-{arctan}^{†}(\frac{x}{y}) \end{aligned}

I took it a step further here by using arctangent’s property as an odd function: $arctan (- x) = - arctan (x)$ . In terms of implementation, this means:

Invert the division by swapping the two arguments^♥.
Flip the output sign of ${arctan}^{†}$ .
Add 90° or 0.25 turns or 16384 brads to the result.

For the other octants, similar transformations can be applied to put them into the valid domain of ${arctan}^{†}$ and results can likewise be rotated back.

Lastly as a detail, the boundary condition $x = y$ needs to be tested for. This is because the result of $\frac{y}{x}$ , 1, can’t be represented in the Q1.0.15 format. Fortunately, the result of atan2 for those cases is obvious. That is, with the exception of $x = y = 0$ , which we just have to test for explicitly and handle as an error.

Book mark §

My derivations here diverged from the four-quadrant formula in the book. I marked these as wrong in 2012, but I’m not so sure they’re different from my implementation when accounting for signed↔unsigned angular output.

Never trust a Canadian — Streamlining DSP table

It looks like the octants IV and V equation accounts for the sign change across the signed atan2 discontinuity. However, since binary angle discontinuity is handled by integer overflow aligned with the output of my atan2, I can handle octants IV and V simply as the 180° rotated version of octants I and VII.

`nabs` rocks §

So anyways, here’s the implementation. I should note that the code relies on a q15_mul function that perform rounding of the product from the 32-bit intermediate to 16-bit result for maximum accuracy. Also, s16_nabs is a function for negative absolute value. Why use nabs? Well, abs is undefined for the most negative number, and chances are if you plug the Q15 value for −1 into abs, you’ll get −1 back out. Negative absolute value, on the other hand, is pretty easy to keep fully defined.

I knew how much theoretical error to expect, but I wasn't sure how to analyze my approximate arctangent's fixed-point implementation. So, I brute-force ran all 2¹⁶ × 2¹⁶ = 4294967296 possible inputs and computed their errors relative to the double-precision atan2 implementation in the GNU C library. I got a worst-case error of 0.221°, which means I’m not losing much precision or introducing quantization error by using fixed-point, and there’s an root mean square (RMS) error of about 0.0004 turns.

s16_nabs, q15_mul, q15_div, and of course fxpt_atan2 are all included in this MIT-licensed source file: fxpt_atan2.c

A DSP library might have faster/better versions of some of those functions that may take advantage of your microcontroller’s DSP ALU.

Codes! §

/**
 * 16-bit fixed point four-quadrant arctangent. Given some Cartesian vector
 * (x, y), find the angle subtended by the vector and the positive x-axis.
 *
 * The value returned is in units of 1/65536ths of one turn. This allows the use
 * of the full 16-bit unsigned range to represent a turn. e.g. 0x0000 is 0
 * radians, 0x8000 is pi radians, and 0xFFFF is (65535 / 32768) * pi radians.
 *
 * Because the magnitude of the input vector does not change the angle it
 * represents, the inputs can be in any signed 16-bit fixed-point format.
 *
 * @param y y-coordinate in signed 16-bit
 * @param x x-coordinate in signed 16-bit
 * @return angle in (val / 32768) * pi radian increments from 0x0000 to 0xFFFF
 */
uint16_t fxpt_atan2(const int16_t y, const int16_t x) {
    if (x == y) { // x/y or y/x would return -1 since 1 isn't representable
        if (y > 0) { // 1/8
            return 8192;
        } else if (y < 0) { // 5/8
            return 40960;
        } else { // x = y = 0
            return 0;
        }
    }
    const int16_t nabs_y = s16_nabs(y), nabs_x = s16_nabs(x);
    if (nabs_x < nabs_y) { // octants 1, 4, 5, 8
        const int16_t y_over_x = q15_div(y, x);
        const int16_t correction = q15_mul(q15_from_double(0.273 * M_1_PI), s16_nabs(y_over_x));
        const int16_t unrotated = q15_mul(q15_from_double(0.25 + 0.273 * M_1_PI) + correction, y_over_x);
        if (x < 0) { // octants 1, 8
            return unrotated;
        } else { // octants 4, 5
            return 32768 + unrotated;
        }
    } else { // octants 2, 3, 6, 7
        const int16_t x_over_y = q15_div(x, y);
        const int16_t correction = q15_mul(q15_from_double(0.273 * M_1_PI), s16_nabs(x_over_y));
        const int16_t unrotated = q15_mul(q15_from_double(0.25 + 0.273 * M_1_PI) + correction, x_over_y);
        if (y > 0) { // octants 2, 3
            return 16384 - unrotated;
        } else { // octants 6, 7
            return 49152 - unrotated;
        }
    }
}