Better Spheres, Fewer Triangles
Generating spheres through recursive subdivision of icosahedrons
UV spheres are one of the easiest and most commmon ways to generate a sphere for computer graphics.
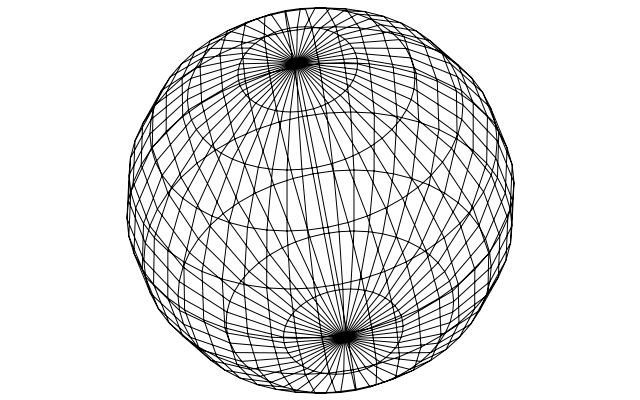
It has its charms: it looks kind of like a globe, with its clear longitudinals and latitudinals, it’s ridiculously easy to imagine and create, and it works well with UV texture mapping. Still, its uneven distribution of points can cause wasted texture resolution as well as computation time at best, funny-looking bunching of points near the “poles” at slightly worse, and disgusting visual artifacts at worst due to having to render many slivers of triangles often of widths less than a pixel.
A far better solution is the geodesic sphere, created by dividing up the faces of a platonic solid and then projecting the vertices onto a sphere*.

To be completed…
*Of course, following this logic, you could make a spherical looking mesh by basically taking any convex mesh and projecting its points onto a sphere. But then its points wouldn’t really be even distributed. That’s why we subdivide an icosahedron.